Python Archives - Blog Geographica

A geodesic (aka geodesic line) is the shortest path between two points located on a given surface. In the world of cartography and geodesy, figure out the shortest path between two locations on an ellipsoid of revolution involves compute a geodesic line joining them (see more in Wikipedia). Consider the Earth as a sphere makes calculations easier, being the shortest path a great circle arc between the points (more on Wikipedia).

For some time, one of the main open source libraries from geo ecosystem, Proj.4, has been introducing major changes in its algorithms for geodetic computations. Specifically, since version 4.9 has been ported to C (inside Proj.4) part of the C ++ library GeographicLib written by Charles Karney (more on algorithms of C. Karney).

Until version 4.8 this library had been using Paul D. Thomas algorithms for Geodesy. The heavy use I make of this library every day has led me to do some testings on geodesic distance calculations. In this link you can access a benchmark I did with several libraries to calculate the geodesic distance between different locations, knowing the coordinates of these locations (which involves figure out the inverse geodetic problem): https://github.com/cayetanobv/GeodeticMusings

Thereafter, and in support of other tasks I was undertaking, I developed a small application which solves inverse geodetic problem based on the above algorithms and computes a geodesic line between start and end points in GIS format directly (Shapefile and/or GeoJSON): GeodesicLinesToGIS.

Is important to highlight that the program efficiently solves the problem of geodesic lines crossing antimeridian (180º) when generating geometries in GIS format. This library is builded on top of three excellent libraries: Pyproj, Fiona and Shapely.

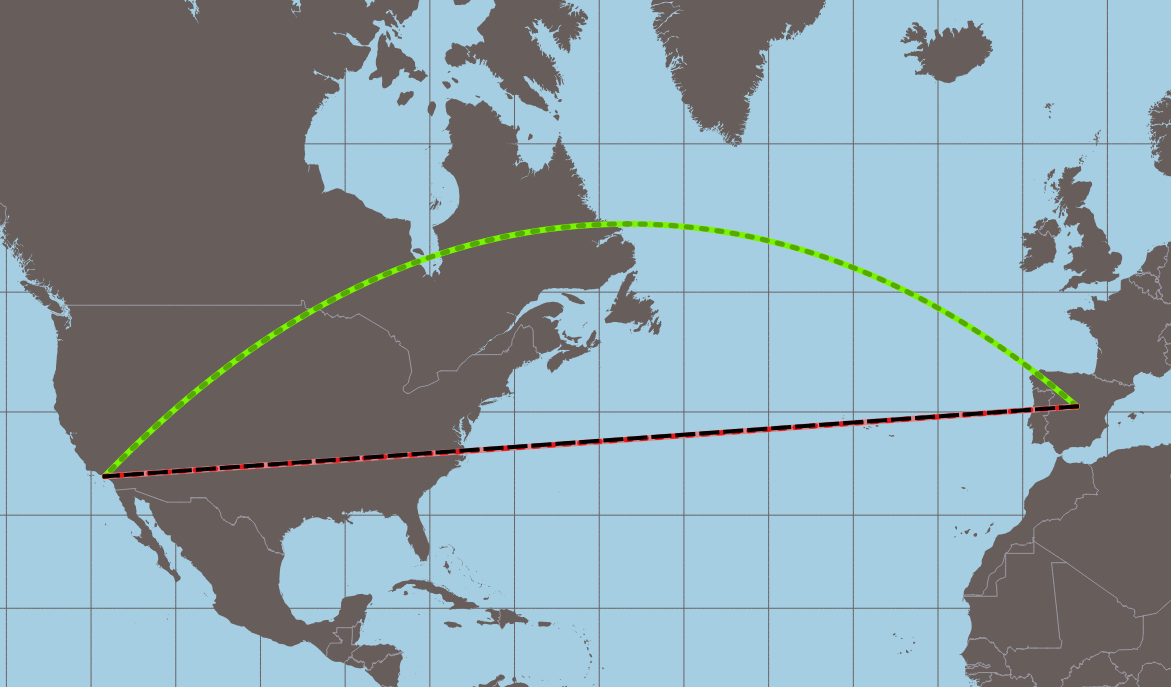
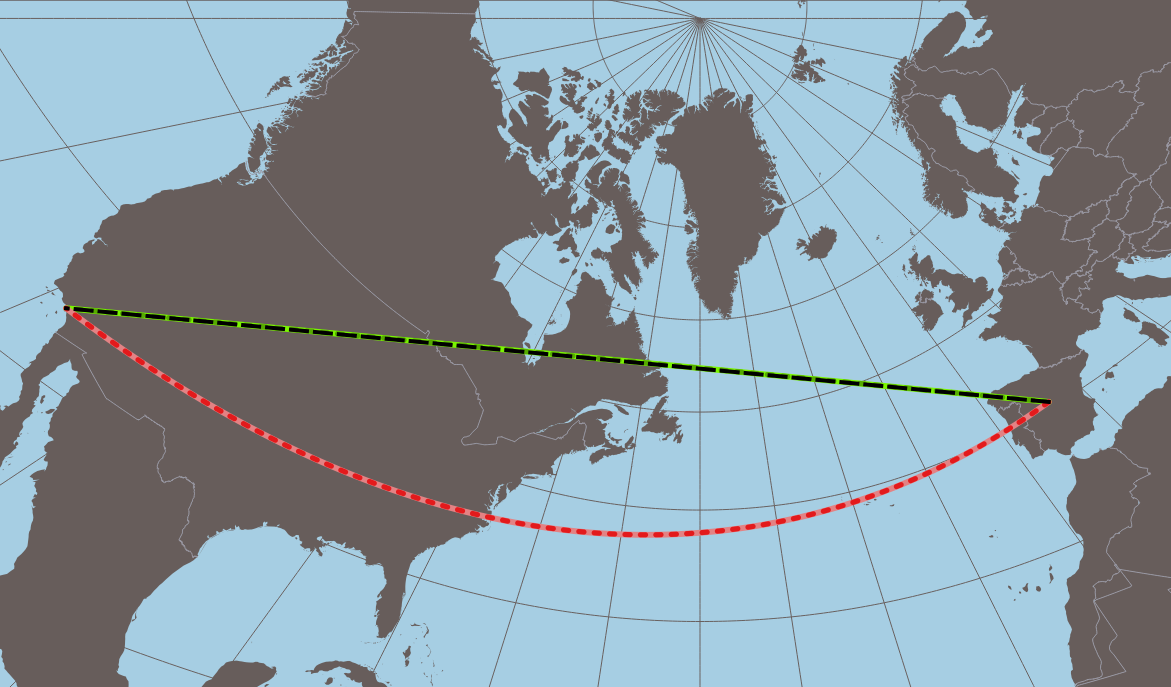
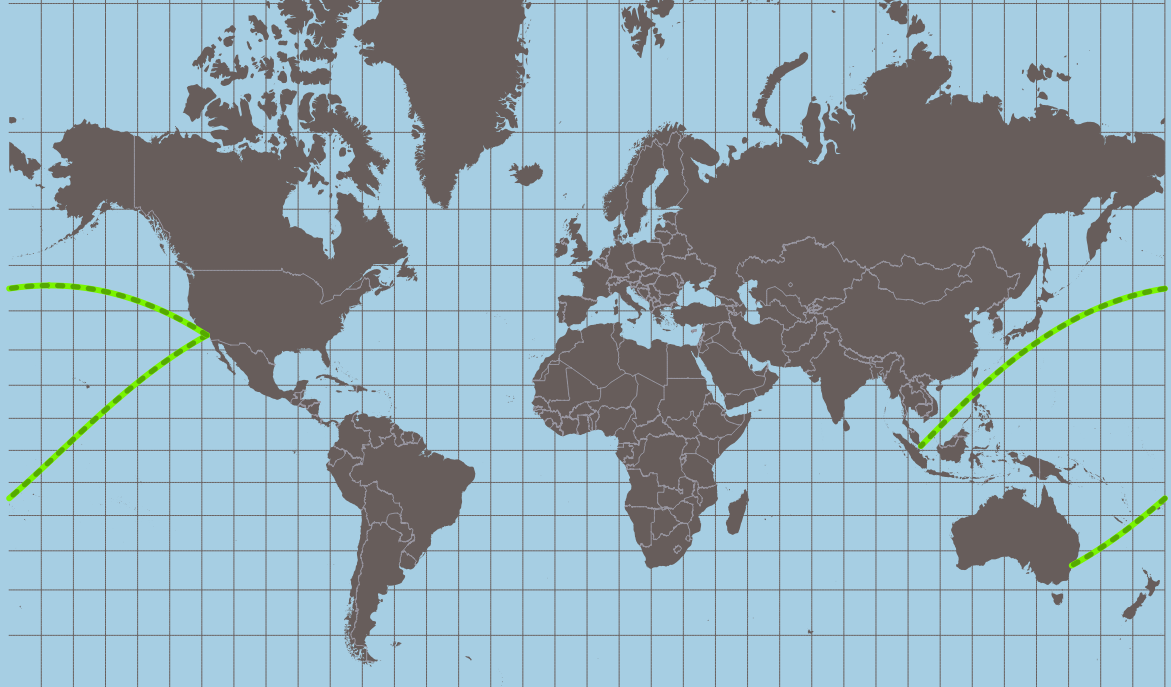
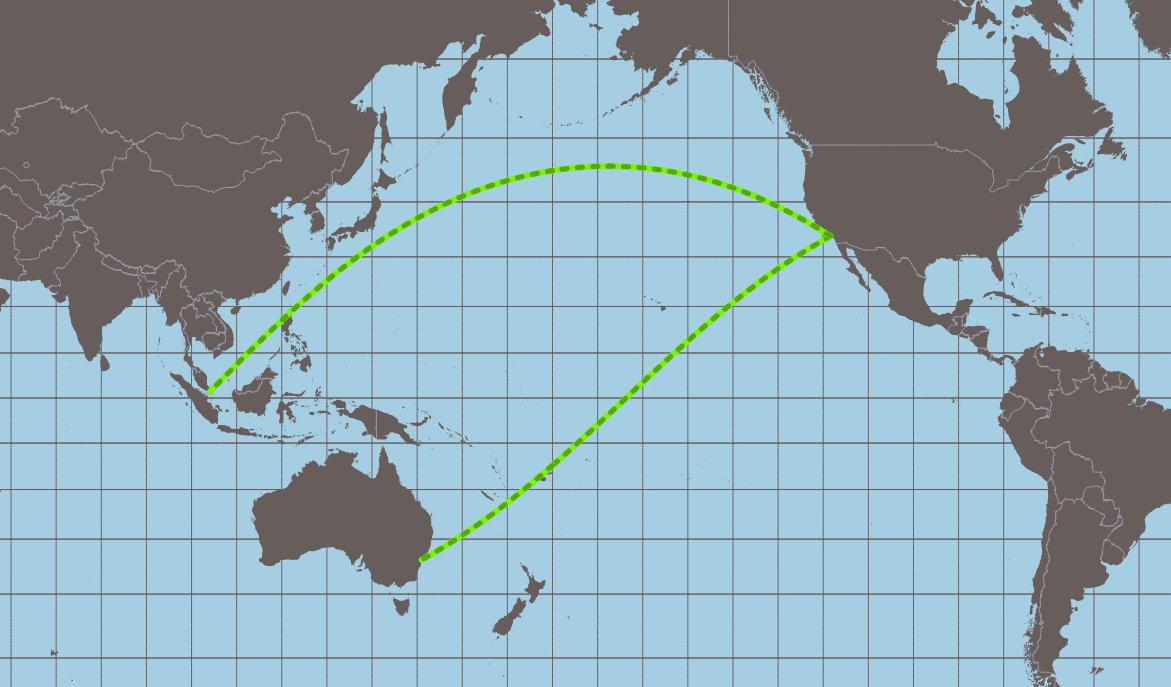
In the examples below you can see the difference between computed geodesic line (shortest path; green line), rhumb line (or loxodromic; red line) and straight line between two points (black dashed line). The maximum differences, as you can expect, occurring between Mercator projection (see Fig 1; loxodromic is a straight line) and Gnomonic projection (see Fig 2; geodesic is a straight line). The problem of geodesic lines crossing 180º is solved, as you can see in Fig 3 and Fig 4.

Fig 1. Mercator Projection: Geodesic lines — Fig 1. Mercator Projection.

Fig 3. Geodesic lines crossing 180º, Mercator Projection.

Fig 4. Geodesic lines crossing 180º, Mercator Projection (Centered on 150ºE).

You can install this package from PYPI (Python Package Index):

https://pypi.python.org/pypi/GeodesicLinesToGIS

Of course, sources are on GiHub:

https://github.com/GeographicaGS/GeodesicLinesToGIS

See you soon!

These past few weeks I have been taking the most out of one of my favorite software libraries for data analysis: Matplotlib. This powefull open-source software library from python-based ecosystem, along with others like Numpy, Scipy, IPython, Pandas, Sympy, etc., is a core package in The Scipy Stack, the Scientific Computing Tools for Python (http://www.scipy.org/).

Although I have been working with Matplotlib for several years, a thorough study of its core has allowed me to slowly get to know their true potential.

Like a geographer, it couldn’t be otherwise Matplotlib toolkit most often used by me is Basemap, which I spent many hours plotting results before include them in a Geographic Information System (GIS). It is noteworthy the strength of Basemap is underpinned by two top quality libraries: PROJ4 and GEOS.

Even though Basemap runs inside Matplotlib, it is a solely library developed by Jeffrey S. Whitaker, a meteorologist from Earth System Research Laboratory – National Oceanic and Atmospheric Administration (NOAA).

It’s a fairy one to remember the importance of Jeffrey S. Whitaker in geoscientific computing world because he has given several very valuable tools to community, like Python binding to Unidata NetCDF C Library or Python bindings to main GRIB file decoders (NOAA and ECMWF).

You can find an example of my last works with Basemap in a tiny library I have developed around it, and I have called daynight2geojson. The aim of this little application is to get worldwide spatial distribution of night at specified date (must be UTC).

If it is not specified a date, this library computes night cover at current date (UTC, of course). When it has been retrieved all data, these are processed and stored in a GeoJSON file. This file could be load in any client capable to read this very simple format (currently most clients can handle this file format without any problem).

All processing are done with the help of Python GeoJSON library and Shapely, a Python library for manipulation and analysis of geometric objects in the Cartesian plane (this library works over GEOS). Output layer Coordinate Reference System (CRS) is EPSG:4326.

For people who want to delve into the subject, all the mathematical background on which is builded the computation of worldwide night geometry are in Basemap solar module: GHA (Greenwich hour angle) computation, solar declination, etc.

Below are displayed some examples of calculations using the library daynight2geojson at different dates: